Energy Levels¶

Energy Quantisation¶

Energy is quantised with Planck’s constant (\(h\)) as the proportionality factor

\[ \begin{align} E&=h\nu\\ E&=h\frac{c}{\lambda}\\ E&=hc\tilde\nu: \hskip{1cm}\tilde\nu=\frac{1}{\lambda} \end{align} \]

Energy Levels¶

Electronic¶

These the quantum electronic states of the molecule

Translational (3 DOF)¶

The molecule as a whole can move in space (as a single unit)

Rotational (linear = 2 DOF nonlinear = 3 DOF)¶

The molecule can rotate in space

Where \(I=\) The moment of inertia of the system (\(I=\sum_{j=1}^nm_j(x_j-x_{cm})^2\) for linear molecules) and the degeneracy of a given level is \(\mathrm{g}_J=2J+1\)

Momentum for nonlinear molecules

For nonlinear molecules, we need to consider the symmetry, as it will have multiple moments of inertia, based on how it rotates

\[ \varepsilon_J=\frac{\hbar^2}{2I}J(J+1):\hskip{1cm}J=0,1,2,... \]

So this looks like:

\[ \begin{matrix} \varepsilon_0=0:&g_J=1\\ \varepsilon_1=\frac{\hbar^2}{I}:&g_J=3\\ \varepsilon_2=\frac{3\hbar^2}{I}:&g_J=5\\ \varepsilon_2=\frac{6\hbar^2}{I}:&g_J=7\\ \varepsilon_2=\frac{10\hbar^2}{I}:&g_J=9\\ \end{matrix} \]

Vibrational (linear = 3n-5 DOF nonlinear = 3n-6 DOF)¶

Note

The subtraction from the degrees of freedom is removing the translational and rotational degrees of freedom. All molecules have a total of \(3n\) degrees of freedom

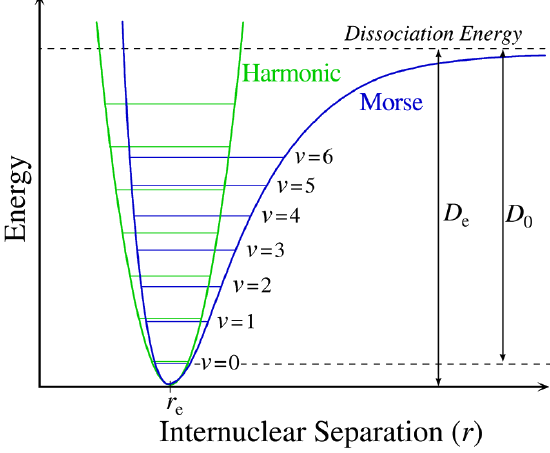
The regions bonds can vibrate with energy

This is a harmonic oscillator model and the degeneracy is \(\mathrm{g}_v=1\)

The space between each of the energy levels is \(=h\nu\), and the first energy level is separated from the depth of the well by the ZPVE \(\bigg(\frac{h\nu}{2}\bigg)\)

\[ \varepsilon_v=h\nu\bigg(v+\frac{1}{2}\bigg)\\ v=0,1,2,... \]

For the Morse potential, we can use the equation

\[ D_e=D_0+\frac{h\nu}{2} \]

The individual vibrations have different normal modes (types of vibration), and so the total vibrational energy is the sum of all the normal modes

\[ \varepsilon_{vib}=\sum\limits_{j=1}^{n_{vib}} h\nu_j\bigg(v_j+\frac{1}{2}\bigg) \]

Total energy¶

The total energy of a molecule can be described as the sum of all of these energies

\[ \epsilon=\epsilon_{trans}+\epsilon_{rot}+\epsilon_{vib}+\epsilon_{elec} \]

Spacing of Energy Levels¶

These energy levels build upon each other, so for every electronic level is a series of vibrational levels and for every vibrational levels there are a series of rotational levels and for every rotational level there are a series of translational levels