Model Chemistry

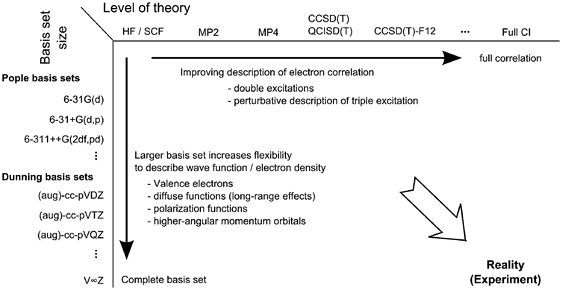
• All quantum chemistry calculations start with HF as a baseline
  • Additional theories can be implemented:
    • Møller-Plesset perturbation theory
    • Configuration Interaction
    • Coupled Cluster
• Everything is a trade off between accuracy (large basis set, higher level of theory) and computational cost/time

• The higher the theory and basis set, the more realistic the results
  • It’s worth noting that DFT

Electron Configuration * We define electron configuration in comp chem much like we do in physical chem * We use symmetry and number the order however, to describe the orbitals * E.g. for water:

\[ 1(A_1 )^2 2(A_1 )^2 1(B_2 )^2 3(A_1 )^2 1(B_1 )^2 4(A_1 )^0 2(B_2 )^0 \]

• We use the terms HOMO and LUMO to describe these and can often describe the surrounding orbitals as HOMO-1 and LUMO+1

Koopman’s Theorem

• States that the ionisation energy of an atom or molecule is equal to the energy from the orbital of which the electron is ejected

\[ I_i=−\epsilon_t \]

• In HF, the energies are more exactly calculated, however in DFT, we can only say that the energy is approximately equal to the ionisation energy (meta Koopman’s theory)

\[ I_i≈−\epsilon_t \]

Coordinates

• The general rule of thumb is that the fewer coordinates there are, the less variables there are for the computer to have to optimise
• The connectivity is determined by the atom’s behaviour, so we don’t need to specify it explicitly
• We can depict geometry in two primary ways:

Cartesian Coordinates

• Use the cartesian system of X, Y and Z values for each atom
• E.g.

  C       x     y     z
  C       x     y     z
  H       x     y     z
  H       x     y     z
  ...
  

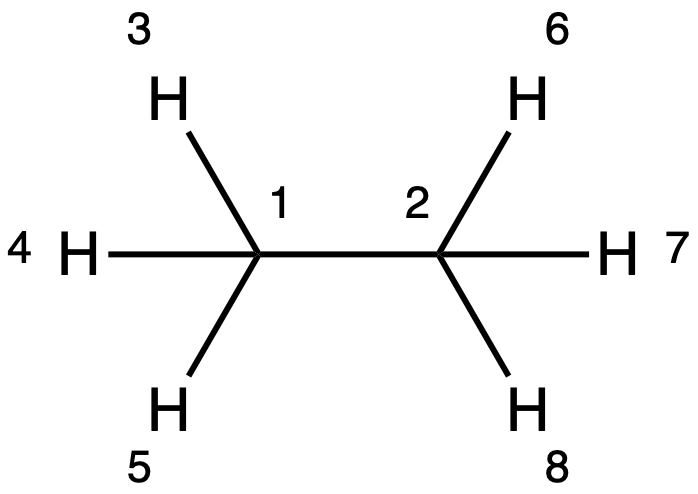
Z-Matrix

• Uses a system of internal coordinates of bond lengths, angles and dihedrals to define the geometry
• E.g.

  C1
  C2     R1     1
  H3     R2     1     𝜃1     2
  H4     R3     1     𝜃2     2     D1     6
  H5     R4     1     𝜃3     2     D2     6
  H6     R5     2     𝜃4     1     D3     3
  H7     R6     2     𝜃5     1     D4     3
  H8     R7     2     𝜃6     1     D5     3
  
  R1=
  R2=
  ...
  𝜃1=
  𝜃2=
  ...
  D1=
  D2=
  ...