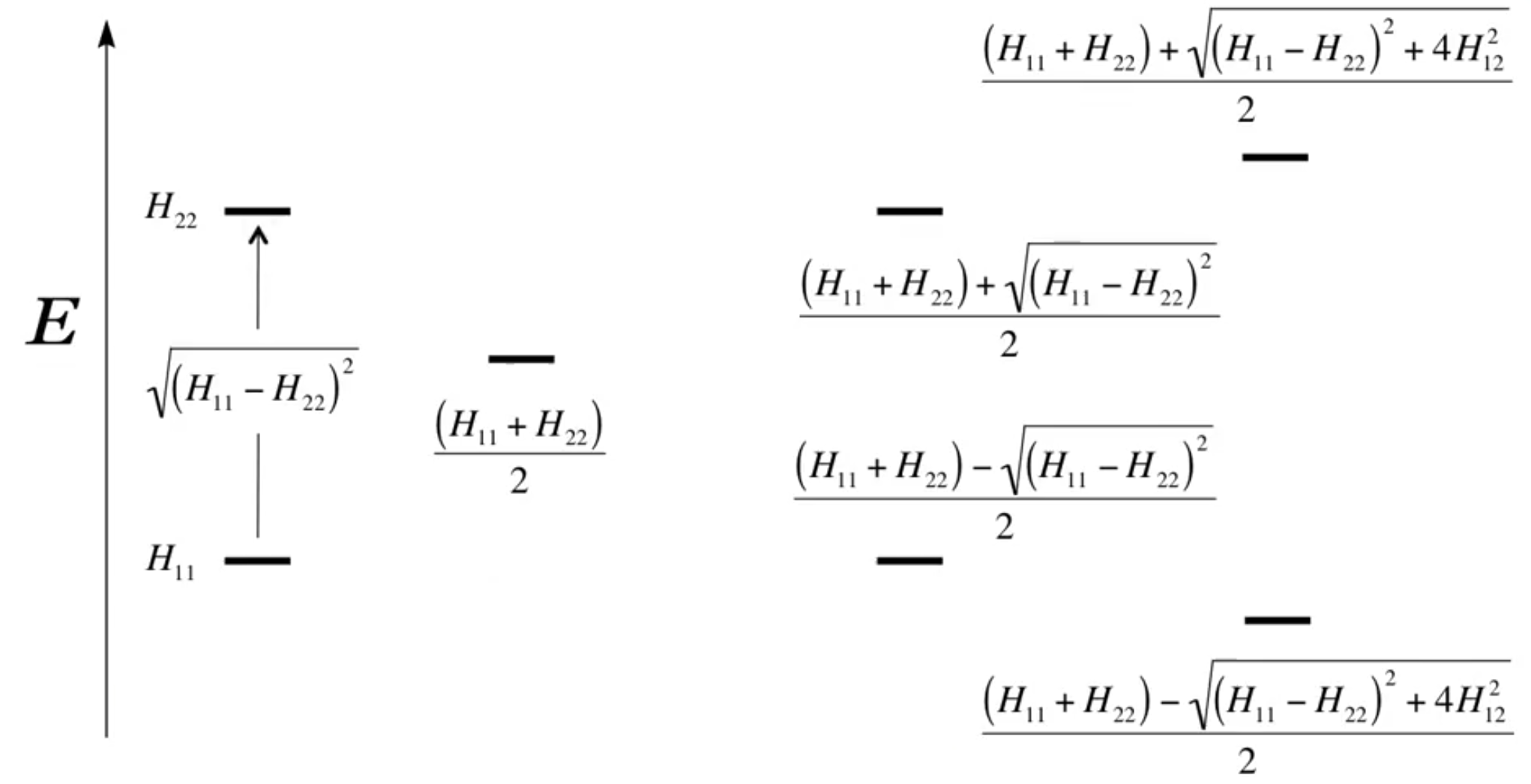Effective Hamiltonians¶
What are the Resonance and Overlap Integrals?¶
Lots of algebra but the gist is:
From our determinant, we have a way to think about what the values mean
\[
\begin{vmatrix}
H_{11}-ES_{11} & H_{12}-ES_{12} & \cdots & H_{1N}-ES_{1N} \\
H_{21}-ES_{21} & H_{22}-ES_{22} & \cdots & H_{2N}-ES_{2N} \\
\vdots & \vdots & \ddots & \vdots\\
H_{N1}-ES_{N1} & H_{N2}-ES_{N2} & \cdots & H_{NN}-ES_{NN}
\end{vmatrix}=0
\]
- The overlap integrals are normalised values (\(-1\) to \(1\)) that measure the nearness and phase relationships between the orbitals
- The resonance integrals on the diagonal give us the energy of each of the MO
- The resonance integrals on the off-diagonal allow for a mixing of orbitals that improve the energy of one orbital at the expense of another
Example
For a 2 basis function system, with zero overlap integrals, our determinant looks like this:
\[
\begin{vmatrix}
H_{11}-E& H_{12}\\
H_{21} & H_{22}-E\\
\end{vmatrix}=0
\]
When we solve this we get:
\[
E=\frac{(H_{11}+H_{22})\pm\sqrt{(H_{11}-H_{22})^2+4H_{12}^2}}{2}
\]
Which we can think of as:
- \(H_{11}/H_{22}=\) The initial MO energy
- \(\sqrt{(H_{11}-H_{22})^2}=\) The difference between the two MOs
- \(\frac{(H_{11}+H_{22})}{2}=\) The middle point between the two MOs
- \(4H_{12}^2=\) A corrective term that allows for the basis functions to mix and provide resonance stabilisation/destabilisaiton