Density Functional Theory¶
Basics¶
- A function takes a number and returns another number
- An operator takes a function and returns another function
- A functional takes a function and returns a number
Rather than putting effort into solving for \(\Psi\) which has far too many variables to be practical, we can make a few inferences and approximations that essentially allow us to calculate the electron density over a grid and allow us to determine what the resulting wavefunction and energy will be
The Hamiltonian is a parameter that can be used to give \Psi
\[
\widehat{H }=\widehat{T}_n+\widehat{T}_e+\widehat{V}_{nn}+\widehat{V}_{ne}+\widehat{V}_{ee}
\]
Through some assumptions made, we can translate this to be in terms of electron density (\(\rho\))
\[
E[\rho]=T[\rho]+E_{ext}[\rho]+E_{coul}[\rho]+E_{xc}[\rho]
\]
- The nightmare of solving for this exchange-correlation interaction becomes a functional of the electron density
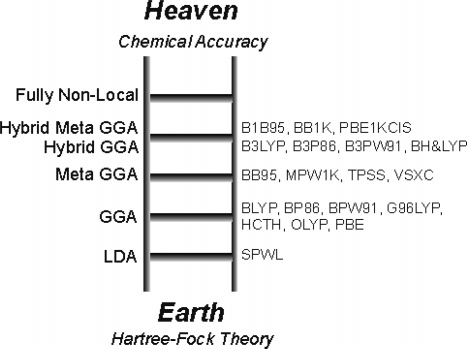
Jacobs Ladder¶
LDA - local (spin) density approximation¶
- \(V_{xc}\) is defined as only depending on the local values of the electron density
- Is good for periodic systems but calculated bond strength and electron correlation to be too big
- E.g. SVWN, VWN5
\[
E_x^{LDA}[\rho]=−c_x\int{\rho^{\frac{4}{3}}(\hat{r})d\hat{r}}
\]
GGA - generalised gradient approximation¶
- \(V_{xc}\) is also includes the first derivative of \(\rho\)
- Is better for molecules
- Builds upon LDA
- E.g. Exchange: PW86, B88, BP88, HCTH
- E.g. Correlation: LYP, PW91, BLYP
\[
E_x^{D88}[\rho]=E_x^{LDA}[\rho]−\beta\rho^{\frac{1}{3}} \frac{x^2}{1+6\beta x sin h^{−1} x′}
\]
Parameters = β, 1+6β
Meta-GGA¶
- Also includes second derivatives for better accuracy
- Not good for all molecules due to limited training set for determination of parameters
- E.g. M06-L, TPSS
Hybrid¶
- Mixes in HF exchange with GGA
- Most popular functionals
- E.g. B97/2,MPW1K
- E.g. B3LYP - 3 parameters; a, b and c
- Hybrid DFT mixes DFT with other post-HF methods to try and combine more concepts in to better account for correlation energy
\[
E_{xc}^{B3}=(1−a) E_x^{LDA}[\rho]+a_x^{HF}+b\Delta E_x^{B88}[\rho]+(1−c) E_c^{LDA}[\rho]+c\Delta E_c^{GGA}[\rho]
\]
Parameters = a, b, c
Hybrid-Meta-GGA¶
- E.g. M05-2X, M06-2x, MPWB1K
- Meta-GGA Hybrid
Running DFT¶
What you need¶
- Molecule geometry
- Molecular charge
- Spin multiplicity (2s+1)
- Basis set
- Exchange functional (S,B,B3 etc..)
- Correlation functional (LYP, PW91 etc…)
Precautions¶
- Different methods and basis sets can yield highly different results
- It is important to know the errors associated with the particular choices of computations
- This is doubly important when looking at someone else’s results
- DO NOT TAKE ANYTHING AT FACE VALUE
Strengths and Weaknesses of DFT¶
- Strengths
- Low computational cost
- Accurate for structures and thermochemistry
- The density is conceptually simpler than \(\Psi\)
- Weaknesses
- Can fail in spectacular and unexpected ways
- There isn’t a systematic way of improving results
- Multidimensional integrals can be problematic
HF vs DFT¶
- DFT is not approximate, it is exact
- Everything we do however is a functional of \(\rho\) which means that the density has to be accurate
- Hohenberg-Kohn proved that the functional of \(\rho\) must exist
- There is no definition as to what the functional should look like
- We know \(f[\rho]\) exists, we just don’t know what it is
Contrast¶
- HF is an approximate theory that solves the relevant equations exactly
- DFT is an exact theory that solves the relevant equations approximately (since we don’t know\(f[\rho]\))
- DFT is not variation due to all the additions, however exact DFT is
About DFT¶
- DFT is good for determining geometries, but not so much for calculating energy
- Totally fails for non-covalent interaction
- Can have large errors for excitation energies
- Fixes include CAM-B3LYP or TD-DFT