MM Force Fields: Part 1¶
Abstract
How do you find a global minimum when there’s so many local minima?¶
- Systematically search all the coordinates?
- Impossible (\(~N^100\))
- Dynamics and quench (MD/Monte Carlo)
- Run a dynamics simulation at a high temperature and periodically cool it down to see which structure it relaxes in to
- Simulated annealing (MD/Monte Carlo)
- Heat the system up and cool it down slowly (similar to dynamics and quench)
- Evolutionary/Genetic Algorithms
- Allow “good” geometries to survive and share properties and “bad” ones to die
- Not a likely option
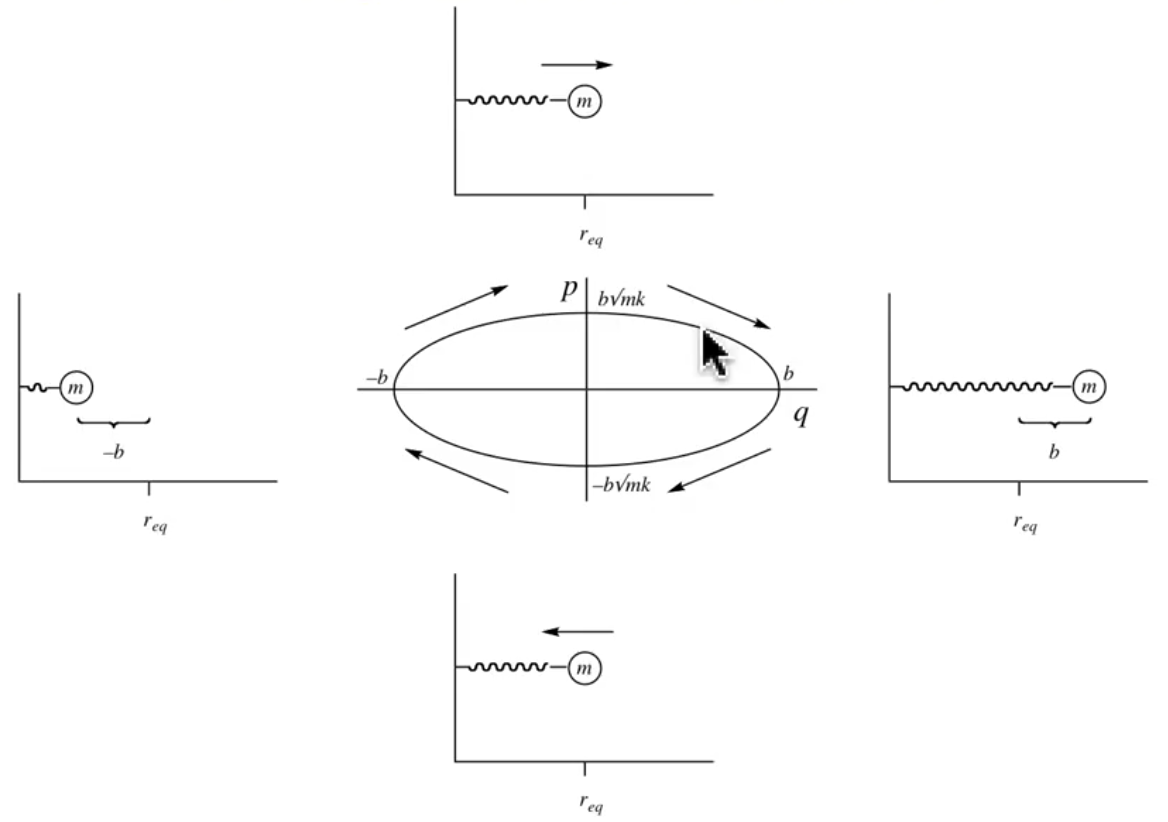
Phase Space¶
The space that’s characterised by the momentum and the position of the particles within the system
- \(r=(q,p)\)
- \(r=(q_{1x},q_{1y},q_{1z},p_{1x},p_{1y},p_{1z},...)\)
In the image below, the middle plot shows the trajectory of momentum (\(p\)) and position (\(q\)). Since it is harmonic, the plot is elliptical
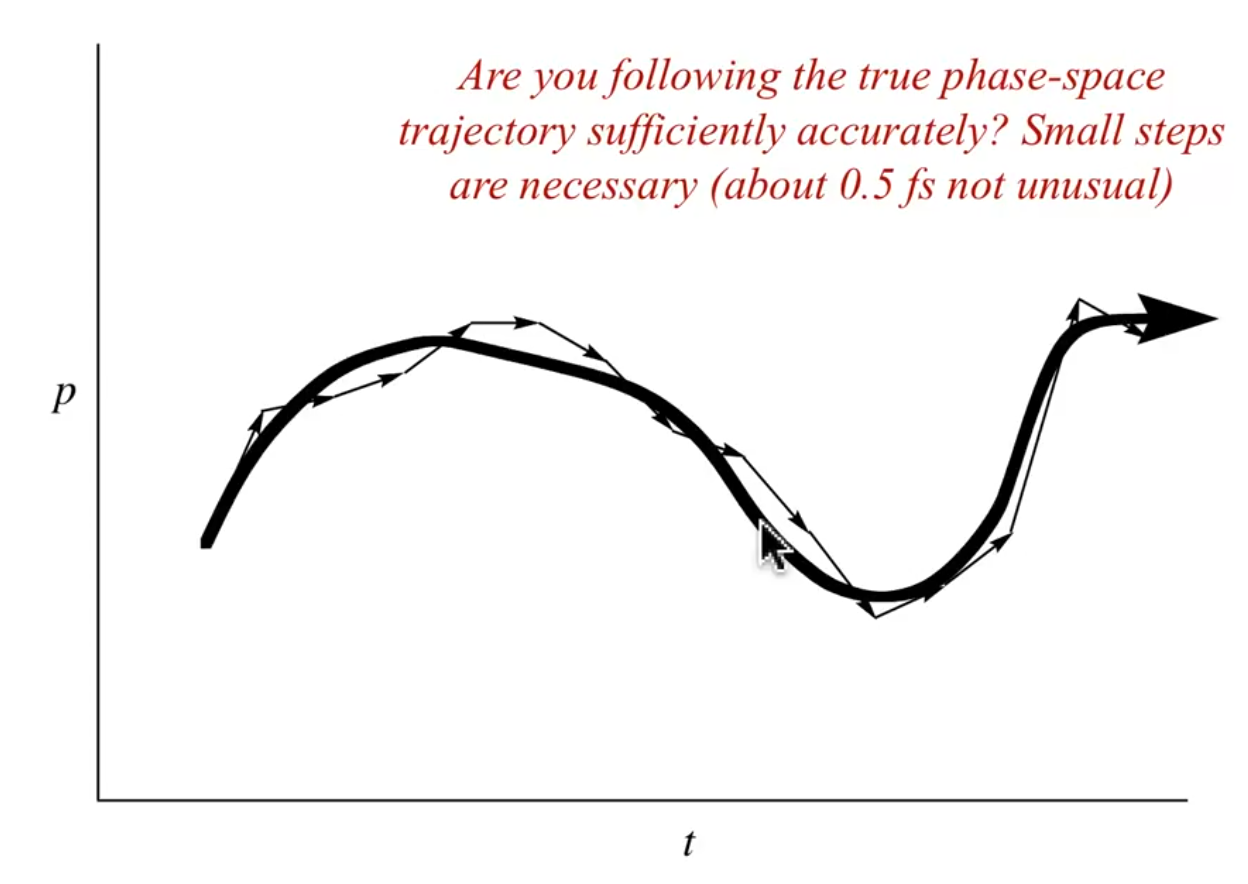
Are you following this phase space in small enough time steps?¶
- If the steps are too big, the trajectory may differ from the realistic (infinitely small) steps taken in reality
- Think, broken physics in games
- The image below shows an example of a normal phase space trajectory