Ab Initio

• Ab initio methods utilise the HF approximations
  • BO approximation - PES
  • HF approximation (mean field approximation) - SCF
  • LCAO

HF Theory

• In HF Theory, the energy of a system is the sum of five different energy terms

\[ E_{HF}=E_T+E_v+E_J+E_K+E_C \]

• \(E_T\) is the electron kinetic energy
• \(E_V\) is the coulombic nuclear-electron attraction energy
• \(E_J\) is the coulombic electron-electron repulsion energy
• \(E_K\) is the electron-electron exchange energy (Energy released when electrons in degenerate orbitals exchange position)
• \(E_C\) is the correlation energy (Results from the instantaneous interaction of electrons and is neglected by the HF approximation)

Note

From the BO approximation, the Hamiltonian term \(\widehat{T_n}\) doesn’t exist (nuclear kinetic energy) and \(\widehat{V_{nn}}\) can be reduced to a constant (\(E_{NN}\))

The Wavefunction

• LCAO is in effect

\[ \Phi_i=\sum{c_{\mu i}\chi_\mu} \]

• \(\Phi_i\)= the molecular orbital
• \(c_{\mu i}\)= the molecular orbital coefficient - a weighted contribution of how much each basis function effects the final molecular orbital
• \(\chi_\mu\)= the basis function
  • The basis function here is \(Ne^{−\zeta r^2}\)
  • \(N\) in the basis set is a normalisation constant \(C_i\) in this unit
  • \(\zeta\) is the exponent, providing the width of the Gaussian function
  • \(r\) is the spacial location of the orbital
  • The amount of zeta determines the amount of functions that can be optimised
    • E.g. Triple \(\zeta\) would be \(\chi=(Ne^{−\zeta_1r^2})+(Ne^{−\zeta_2r^2})+(Ne^{−\zeta_3r^2})\)

E.g.

\[ \Phi_1=(c_{1,1}\cdot \chi_1 )+(c_{2,1}\cdot \chi_2 )+(c_{3,1}\cdot \chi_3 )+(c_{4,1}\cdot \chi_4 ) \]

\[ \Phi_2=(c_{1,2}\cdot \chi_1 )+(c_{2,2}\cdot \chi_2 )+(c_{3,2}\cdot \chi_3 )+(c_{4,2}\cdot \chi_4 ) \]

Electron Spin

• We also need to consider the spin of electrons (\(\alpha\) and \(\beta\))
• In closed shell systems (systems where all the electrons are paired in orbitals, \(\alpha\) and \(\beta\) electrons have the same spacial coordinates (\(r\)) for simplicity
• In open shell systems we need to be a bit more careful with this

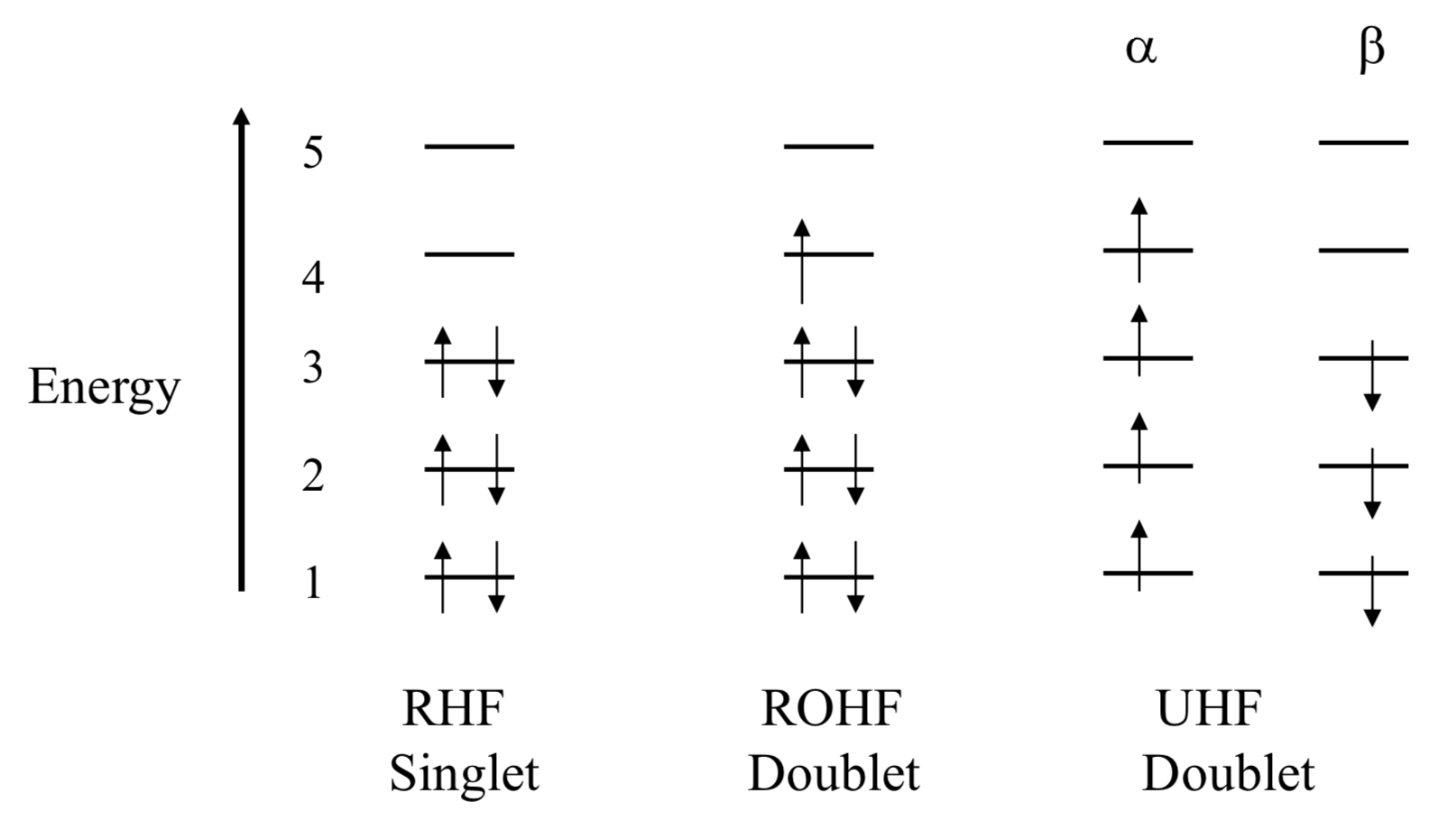
RHF/ROHF/UHF

• Restricted Hartree-Fock (RHF)
  • For closed shell systems all the spin up and spin down orbitals have the same spatial coordinates
    
    
• Restricted Open-Shell Hartree-Fock (ROHF)
  • All paired electrons are treated are RHF and any unpaired electrons have different functionals for the occupied component and the unoccupied virtual component
    
    
• Unrestricted Hartree-Fock (UHF)
  • All electrons are considered to have their own orbital, without considering paired and unpaired electrons in the same orbital

Advantages and Disadvantages of UHF

• Advantages
  • Accounts for the influence that unpaired electrons have on the paired electrons
    • They have a habit of changing spin densities
  • Provides qualitatively description of bond breaking/forming
  • Models open shell systems more accurately than RHF

• Disadvantages
  • Computationally more expensive
  • Can lead to spin contamination - where the wavefunction isn’t always made of one spin up and one spin down electron. This leads to an improper wavefunction being formed

Electron Correlation

• An inherent error within HF neglects a portion of the energy of the system. This is known as correlation error
• Of the three remaining Hamiltonian terms after the BO approximation, they are broken down as such

\[ \widehat{T}_e+\widehat{V} _{ne}=E_T+E_V \]

\[ \widehat{V}_{ee}=E_J+E_K+E_C \]

• Where:
  • \(E_T\)= electron kinetic energy
  • \(E_V\)= electron potential energy
  • \(E_J\)= coulombic repulsion energy
  • \(E_K\)= exchange energy
  • \(E_C\)= correlation energy
    
    
• Correlation energy is always negative as it’s the process by which electrons minimise their energy
• Is sensitive to the amount of electron pairs and comes in two types
  • Dynamic Correlation - which is the dance that electrons make to try and avoid each other
  • Static Correlation - is the energy associated with electrons being able to change their configuration as needed to minimise their energy (accounted for in CI)
• Calculating this is the single most important thing in quantum chemistry

Møller-Plesset

• Perturbation methods like MP theory assume that the problem we’d like to solve differs only slightly from a problem that we’ve already solved
• The energy is calculated to various orders of approximation
  • MP2 - second order
  • MP3 - third order
  • Etc..
• The computational cost greatly increases with each successive order
• The series is not even guaranteed to converge. * The job may never finish and unlike SCF will not necessarily give you an error
• In general only MP2 is recommend
• MP2 approximately includes single and double excitations

Configuration Interaction

• To account for this, the next generation of ab initio methods accounts for this and are called “post HF methods”
• One of the ways this works is to look at Configuration Interaction (CI)
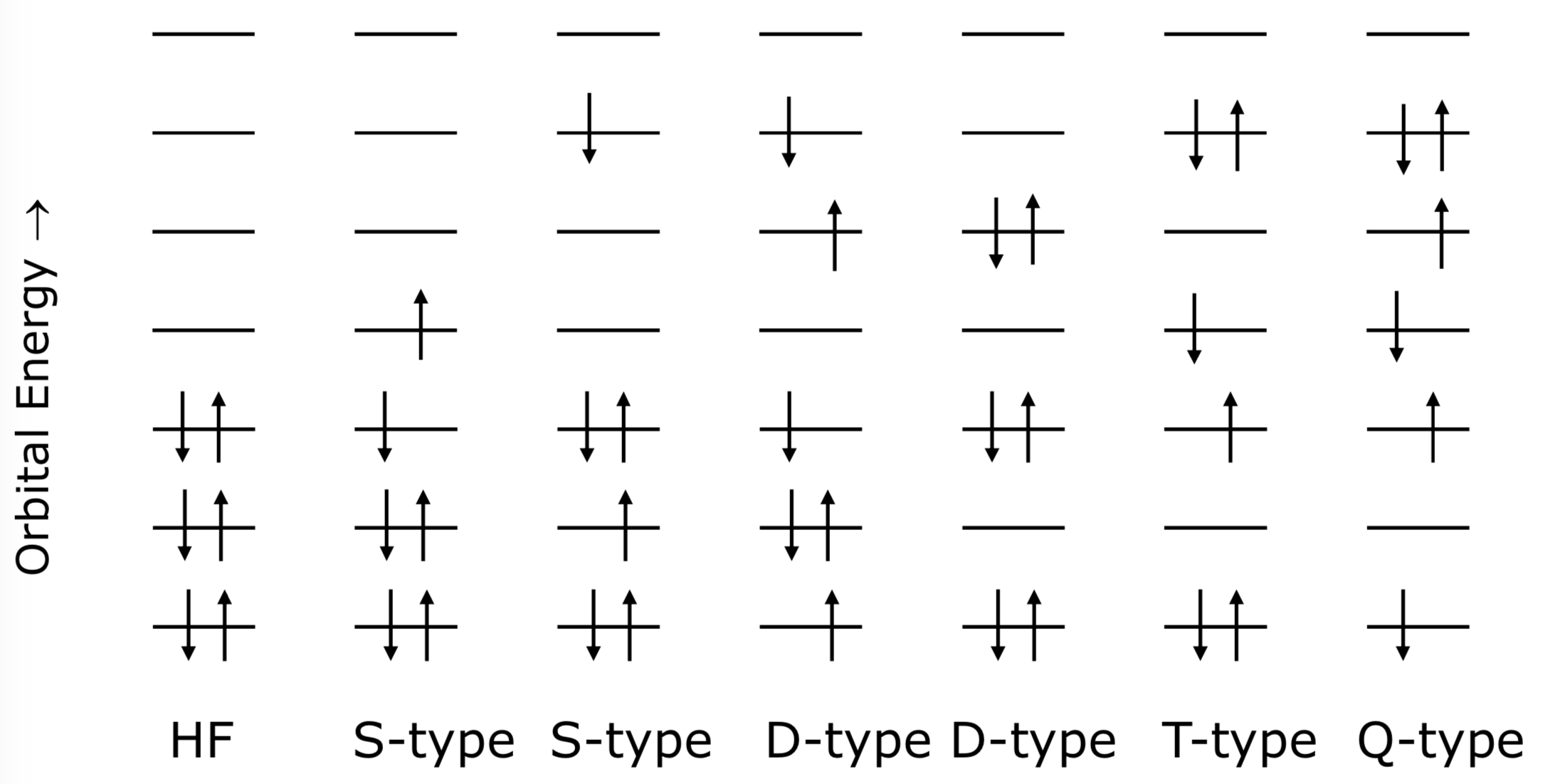
  • This theory considers that the actual composition of a quantum system accounts for all the possible “configurations” (determinants). In this case, that means that a linear combination of all the possible configurations needs to be calculated to account for this process.

    Single           Double        Triple       Quadruple

This number is the amount of electrons that are excited in the process

Coupled Cluster

Rather than using a linear combination of configurations like in CI, CC uses exponential expansion

In CI, we start with the HF determination of the wavefunction \(\Phi\) and correct it with a linear combination of terms calculated from the different determinants (in CI, this operator is denoted C)

\[ \Psi_{CI}=(1+C_1+C_2+C_3+…) \Psi_{HF} \]

In CC, a similar correction is applied but uses the Taylor series to get there (in CC, this operator is denoted \(T\))

\[ \Psi_{CC}=exp(1+\widehat{T}_1+\widehat{T}_2+\frac{1}{2!} \widehat{T}_1^2+\frac{1}{2!} \widehat{T}_2^2+\frac{1}{3!} \widehat{T}_1^3+\frac{1}{3!}\widehat{T}_2^3+…) \Psi_{HF} \]

• The subscript on each operator is the amount of excited electrons
• In “Full CI” all electrons are distributed among all the orbitals as massive cost, so it is common to “truncate” the process and limit it to a certain number of excited electrons

Frozen Core Approximation (FC)

• Since correlating electrons is such a costly and time consuming process, freezing the core electrons which have a mostly negligible impact on the bonding of a molecule can save a huge amount of time
• This is mostly applicable for first row elements atoms as the higher up, the more electrons there are and the more they can interact.
• Some processes rely on core electrons though, so it is really important to understand what you’re doing

By default MP# calculations freeze the core, and to overcome this you need to add mp2(full)

Cost

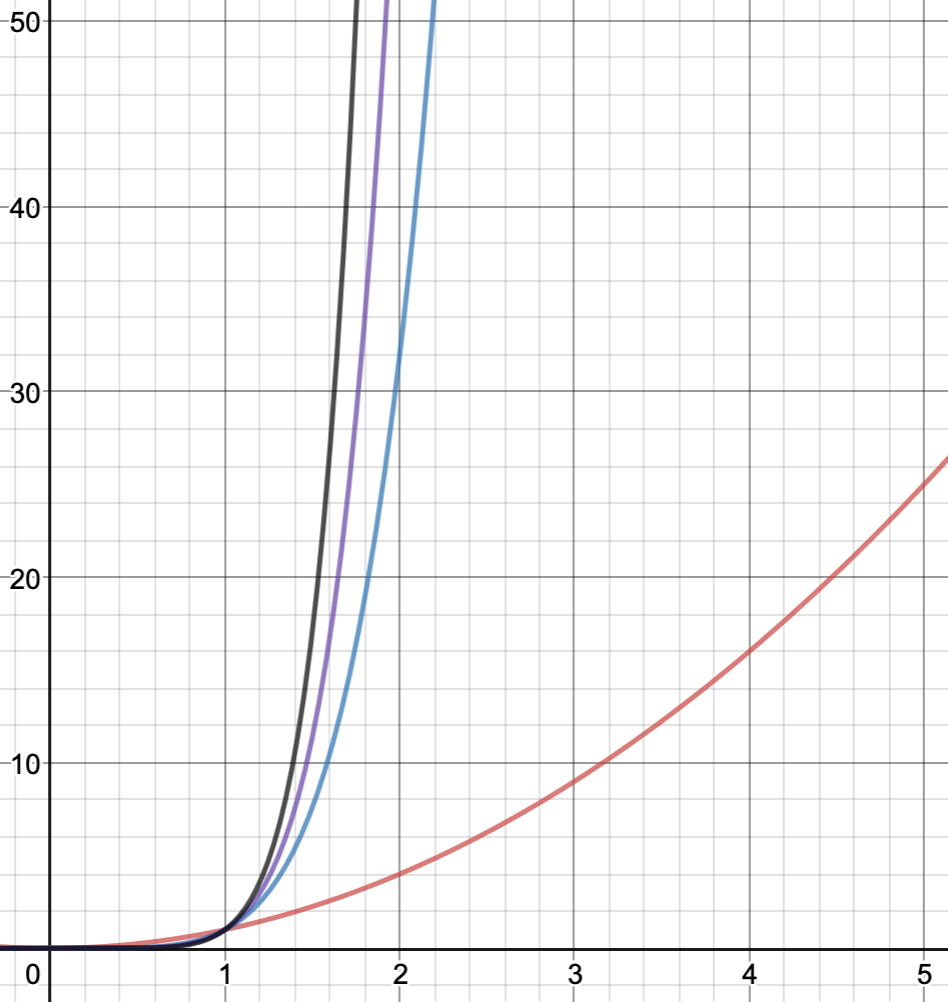
As a comparison, here is a cost table of how computational time where \(N=\) the number of basis functions

• DFT is similar to HF (~\(N^3\))
  

Method	Scaling Cost
HF	N^2
MP2	N^5
CCSD	N^6
CCSD(T)	N^7

• While CISD is an approach that can be used, it has a few shortfalls that make it inefficient
  • QCISD fixes these issues but is more costly than CCSD which is more accurate
  • “CISD is not sufficient, CISDTQ is too expensive “

Semiempirical Methods (AM1, PM3, RM1, etc.)

• Make a fair few simplifications
  • Only look at the valence electrons, so as to minimise the amount of functions needed
  • Don’t look at long range interactions
    • Really important in protein modelling, as there is just far too much going on to account for everything
  • Parameterise lots of properties using experimental results
    • Be aware that these are often trained, and thus may not account for systems outside of the training dataset
    • Also only limited to ground state applications for the same reason
  • Use a minimal basis set, such as 3-21G
  • Employ a non iterative solution process, that is it won’t use guess and check methods such as with SCF